Método de Ordenamiento Merge Sort en C#
Esta vez estaremos hablando de Ordenación por Mezcla (Merge Sort), otro algoritmo recursivo bastante eficiente para ordenar un array, que tiene un orden de complejidad O(nlogn) al igual que Quick Sort. Fue desarrollado en 1945 por John Von Neumann según wikipedia.Estrategia de Merge Sort
Merge Sort está basado en la técnica de diseño de algoritmos Divide y Vencerás, de la cual se habló aquí mismo hace un tiempo. Recordando un poco, esta técnica consiste en dividir el problema a resolver en sub problemas del mismo tipo que a su vez se dividirán, mientras no sean suficientemente pequeños o triviales.
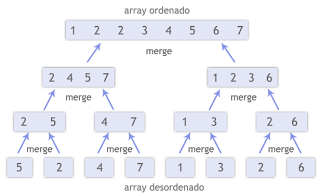
Veamos una panorámica de la estrategia que sigue este algoritmo para ordenar una secuencia S de n elementos:
- Si S tiene uno o ningún elemento, está ordenada
- Si S tiene al menos dos elementos se divide en dos secuencias S1 y S2
- S1 contiene los primeros n/2 elementos y S2 los restantes
- Ordenar S1 y S2, aplicando recursivamente este procedimiento
- Mezclar S1 y S2 en S, de forma que ya S1 y S2 estén ordenados
- Veamos ahora como sería la estrategia para mezclar las secuencias:
Se tienen referencias al principio de cada una de las secuencias a mezclar (S1 y S2). Mientras en alguna secuencia queden elementos, se inserta en la secuencia resultante (S) el menor de los elementos referenciados y se avanza esa referencia una posición.
Pseudocódigo del Método de Ordenamiento Merge Sort
Como ven, la idea es bastante simple, pero programarla no tanto. Para no dar de golpe la solución, veamos primero un pseudocódigo del algoritmo:
function mergesort(array A[x..y])
begin
if (x-y > 1)):
array A1 := mergesort(A[x..(int( x+y / 2))])
array A2 := mergesort(A[int(1+(x+y / 2))..y])
return merge(A1, A2)
else:
return A
end
function merge(array A1[0..n1], array A2[0..n2])
begin
integer p1 := 0
integer p2 := 0
array R[0..(n1 + n2 + 2)]//suponiendo que n1 y n2 son las posiciones
//del array y no el length de este mismo, de otro modo seria (n1 + n2)
while (p1 <= n1 or p2 <= n2):
if (p1 <= n1 and A1[p1] <= A2[p2]):
R[p1 + p2] := A1[p1]
p1 := p1 + 1
else
if (p2 <= n2 and A1[p1] > A2[p2]):
R[p1 + p2] := A2[p2]
p2 := p2 + 1
return R
end
Ejemplo del Método de Ordenamiento Merge Sort en C#
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace MergeSort
{
class Program
{
static void Main(string[] args)
{
int[] nums = new int[40];
Console.WriteLine("Metodo de Merge Sort");
Console.Write("Cuantos longitud del vector: ");
string linea;
linea = Console.ReadLine();
int cant;
cant = int.Parse(linea);
nums = new int[cant];
for (int f = 0; f < nums.Length; f++)
{
Console.Write("Ingrese elemento " + (f + 1) + ": ");
linea = Console.ReadLine();
nums[f] = int.Parse(linea);
}
MergeSort(nums);
Console.WriteLine("Vector Ordenado Ascendentemente");
for (int i = 0; i < nums.Length; i++)
Console.Write(nums[i] + " ");
Console.ReadLine();
}
//Método portal que llama al método recursivo inicial
public static void MergeSort(int[] x)
{
MergeSort(x, 0, x.Length - 1);
}
static private void MergeSort(int[] x, int desde, int hasta)
{
//Condicion de parada
if (desde == hasta)
return;
//Calculo la mitad del array
int mitad = (desde + hasta) / 2;
//Voy a ordenar recursivamente la primera mitad
//y luego la segunda
MergeSort(x, desde, mitad);
MergeSort(x, mitad + 1, hasta);
//Mezclo las dos mitades ordenadas
int[] aux = Merge(x, desde, mitad, mitad + 1, hasta);
Array.Copy(aux, 0, x, desde, aux.Length);
}
//Método que mezcla las dos mitades ordenadas
static private int[] Merge(int[] x, int desde1, int hasta1, int desde2, int hasta2)
{
int a = desde1;
int b = desde2;
int[] result = new int[hasta1 - desde1 + hasta2 - desde2 + 2];
for (int i = 0; i < result.Length; i++)
{
if (b != x.Length)
{
if (a > hasta1 && b <= hasta2)
{
result[i] = x[b];
b++;
}
if (b > hasta2&& a <= hasta1)
{
result[i] = x[a];
a++;
}
if (a <= hasta1&& b <= hasta2)
{
if (x[b] <= x[a])
{
result[i] = x[b];
b++;
}
else
{
result[i] = x[a];
a++;
}
}
}
else
{
if (a <= hasta1)
{
result[i] = x[a];
a++;
}
}
}
return result;
}
}
}